Creating My First Sudoku Puzzle
Like many fellow Sudoku enthusiasts, I began my Sudoku journey during COVID when the Youtube algorithm decided to recommend me a video from the “Cracking the Cryptic” channel (if you’re into puzzles, I highly recommend checking it out!). I remember reading the video title, seeing that the video had hundreds of thousands of views, and thinking: How could a Sudoku puzzle possibly be this interesting? But from the moment that Simon (one of the two people running the channel) read the rules of the puzzle, it became clear that this wasn’t just about your regular-old Sudoku. This was the wonderful world of human-engineered Sudoku variant puzzles. And after Simon finished his solve, my mind was blown: I was hooked.
Down the rabbit hole
Over the next few weeks, I spent many afternoons watching Simon & Marks videos’ about them solving more puzzles. It became something that I did when I wanted to relax and just tag along for an interesting journey down Sudoku-world. I learnt about the different rules that people had come up with, and about Sudoku setters (people that create/set Sudoku puzzles). Setting my own Sudoku became something that I thought about every now and then. What rules would I put in my own Sudoku? How would I even know that it’s possible to create a Sudoku with those rules? How do you even test that? Is there software that setters use? And so on, and so on.
One day, I was working on a problem at work. There was a really elegant solution that involved co-prime numbers. Just for clarification: Two natural numbers are co-prime if they don’t share any divisors (except 1). For example, 15 and 8 are co-prime because 15 is divisible by 3 and 5, but 8 is only divisible by 2 (or 4). And this question popped into my head: Could you make a Sudoku where every pair of neighboring digits is co-prime?
The Coprimality constraint
So, I sat down and thought about this constraint a bit more. First of all, let’s clear up what “neighboring digits” means. In Sudoku-land we call it “orthogonally adjacent”, which Simon likes to explain as “cells that share an edge”. So for cells in the middle of the gird, it’s the four cells that are: above, below, left, and right. Cells on the border have only three neighbors and the cells in the corner of the grid only have two.
Now if we look at the Sudoku digits (1 through 9) and think about what the possible neighbors could be, we can write this into a table to get a better overview. Note that we’re also keeping Sudoku rules in mind so neighboring digits can never be the same.
| Digit | Possible Neighbors |
|---|---|
| 1 | 2, 3, 4, 5, 6, 7, 8, 9 |
| 2 | 1, 3, 5, 7, 9 |
| 3 | 1, 2, 4, 5, 7, 8 |
| 4 | 1, 3, 5, 7, 9 |
| 5 | 1, 2, 3, 4, 6, 7, 8, 9 |
| 6 | 1, 5, 7 |
| 7 | 1, 2, 3, 4, 5, 6, 8, 9 |
| 8 | 1, 3, 5, 7, 9 |
| 9 | 1, 2, 4, 5, 7, 8 |
We can see that 6 is the most constrained digit. It’s divisible by 2 and 3 so it can only go next to 1, 5, and 7. Additionally, we can see that even digits can only go next to odd digits.
If we take the classic 9x9 Sudoku grid and we mark every other cell we get this:

Now knowing that the even digits can only go next to the odd digits, the even digits must go either into the marked squares or the unmarked squares. So let’s see if we can find the places that our 6 can go in the middle box.
Where to put the 6?
Hopefully you can see why a 6 could never go in the cell in the middle of that central box. There are four surrounding cells that all have to be different because of the rules of Sudoku. But we can only put 1, 5, and 7 next to 6. So we would have to repeat a digit and it would break.
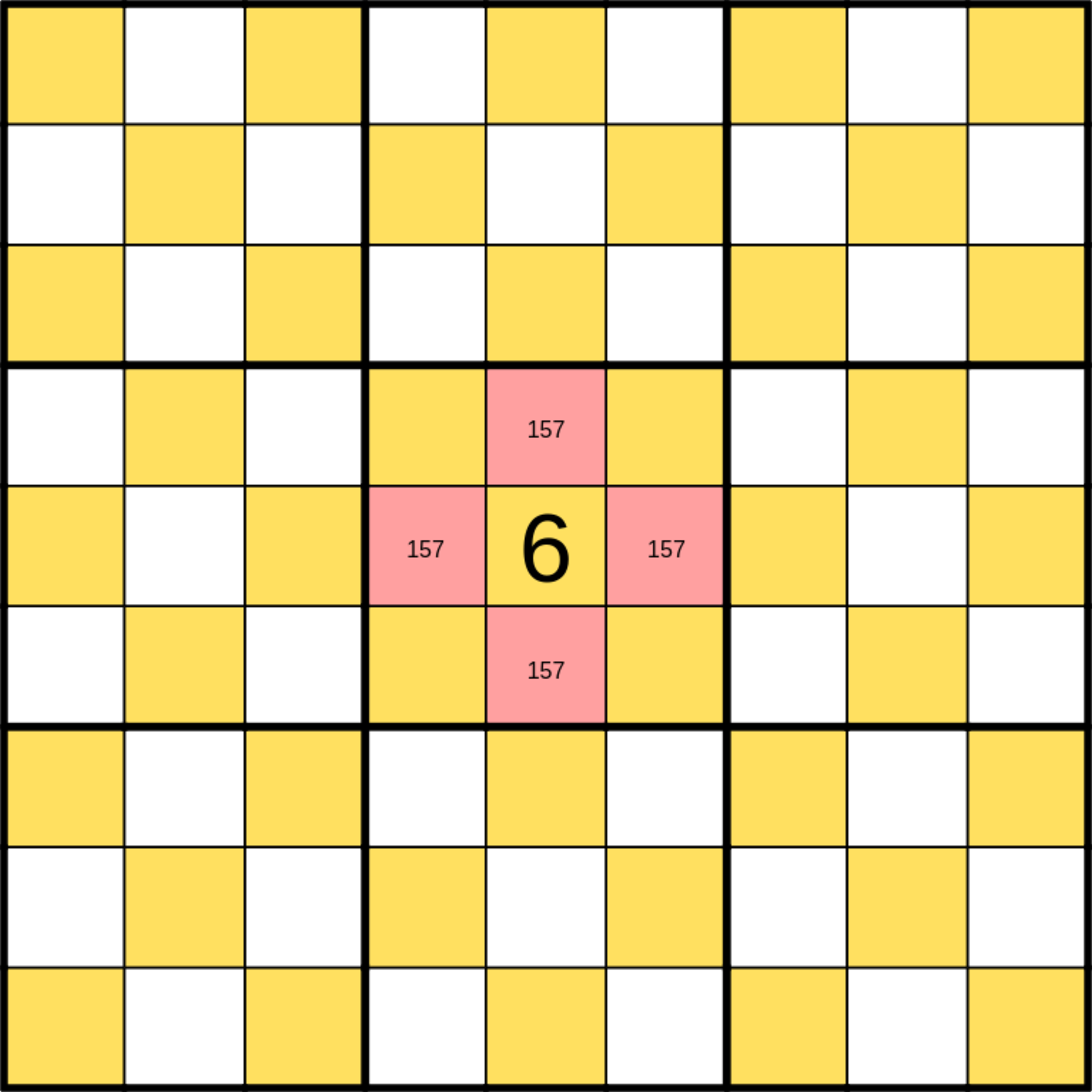
What about the cells on the edges of the box then?
Let’s say we put it in the upper middle cell. By symmetry, the same will apply to all other cells on the edge of the box.
Ok so for the middle box, this would work. There are only three surrounding cells in the same box. And the other neighboring cell is not in the same box, so we can repeat one of the 1, 5, or 7. But let’s look at where the 6 would go in the other boxes.
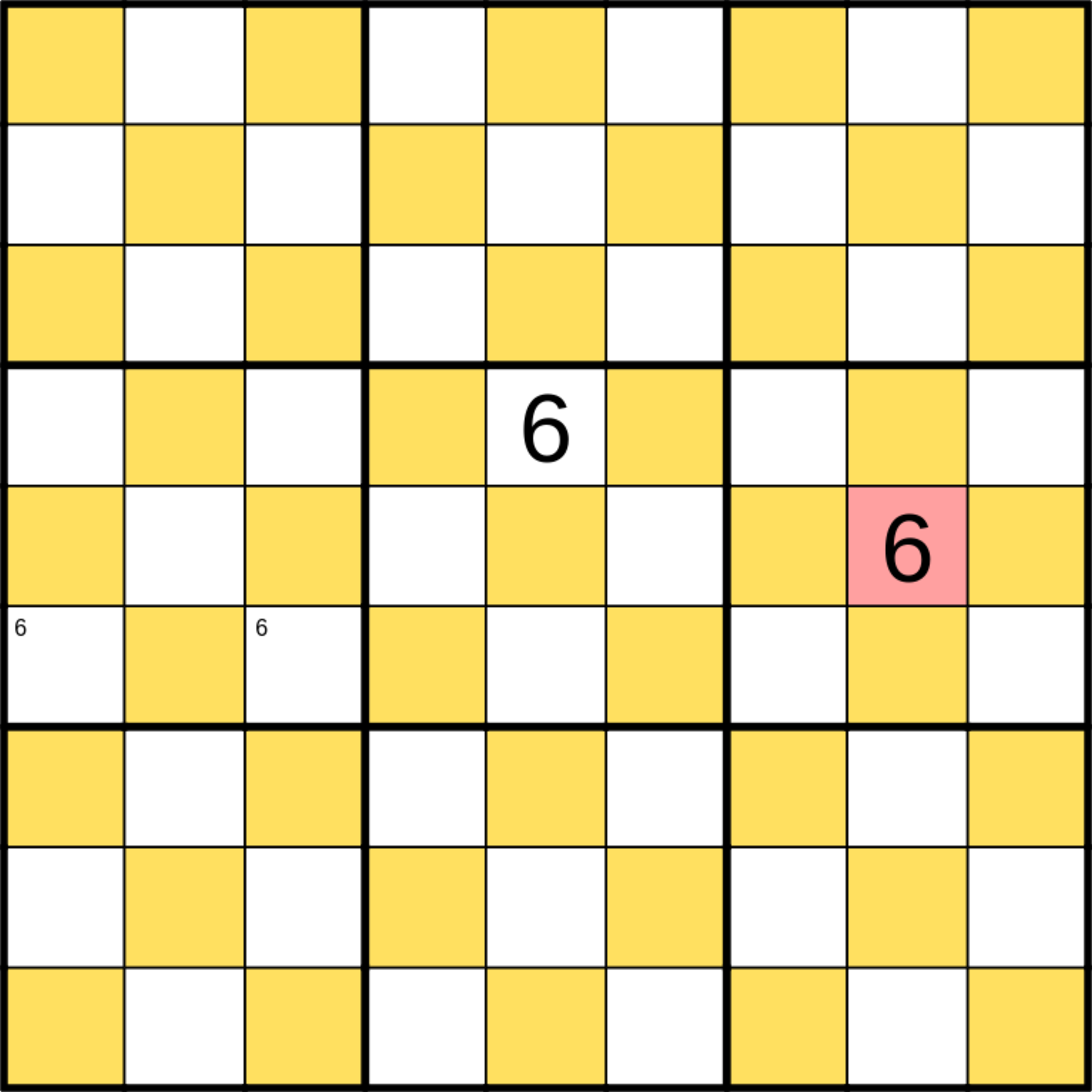
In the box to the left and to the right, no matter how we do it, we’ll end up with a 6 in the middle of a box. Remember that the 6 can only go in the same (unmarked, in this case) group of cells. So this breaks as well!
What about the corner cell in the middle box then?
Again, no matter which corner we try, by symmetry, the same will apply to the other corners as well.

If we look at the neighboring boxes again, the 6 doesn’t have many places to go. E.g. in the image above, we can see that the 6 can’t go on the left edge because there would be four different cells (because they are in the same box) that would have to contain digits from 1, 5, and 7, causing a repeated digit. The same would happen if we put the 6 on the lower middle cell in the left box.
The only place for a 6 in the left box is the right edge. By symmetry we can repeat the same steps for the box above the middle box. We get this:
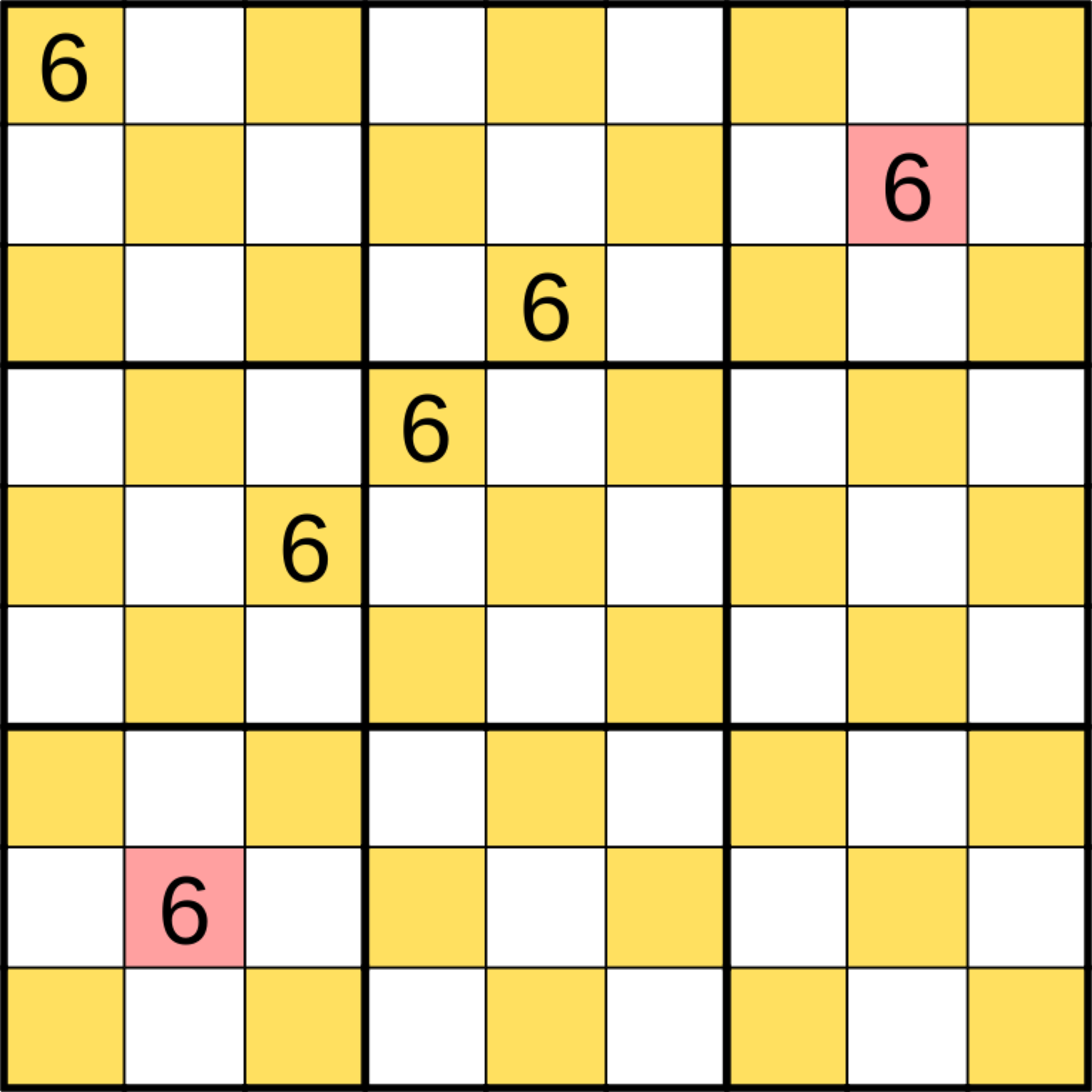
But in the top left box, the 6 now has to go into the corner (it can never go into the center of a box). And we end up with 6s in the center of the top right and bottom left box. Again, it breaks!
We’ve now shown that none of the cells in the center can contain a 6. That means the coprimality constraint can’t work for a 9x9 Sudoku.
Other Sudoku grid sizes
Of course I started to think about other ways of making the constraint work. E.g. you could turn it something that only applies to some cells and not the whole grid. But nonetheless, I thought I would try other grid sizes.
Ideally, we would go up to a 10x10. That means that there are more numbers and therefor more pairs that would lead to interesting interactions with the coprimality constraint. But, for the sake of simplicity, I decided to try out an 8x8 first. This turned out to work quite well (albeit less difficult because there are less pairs). And after only a few minutes of playing with it I had something. I just needed to add some more constraints to make the puzzle have only one solution.
I opted for a common constraint that setters and solvers are familiar with: Arrows! The rules for them are simple: The digits along the arrow sum to the digit in the circle that sits at the start of the arrow. This allowed me to constrain the puzzle further. Finally I added one given digit which made the puzzle have a unique solution.
I’m not going to spoil how to solve it here, but knowing how I approached the 9x9 version should give you enough information.
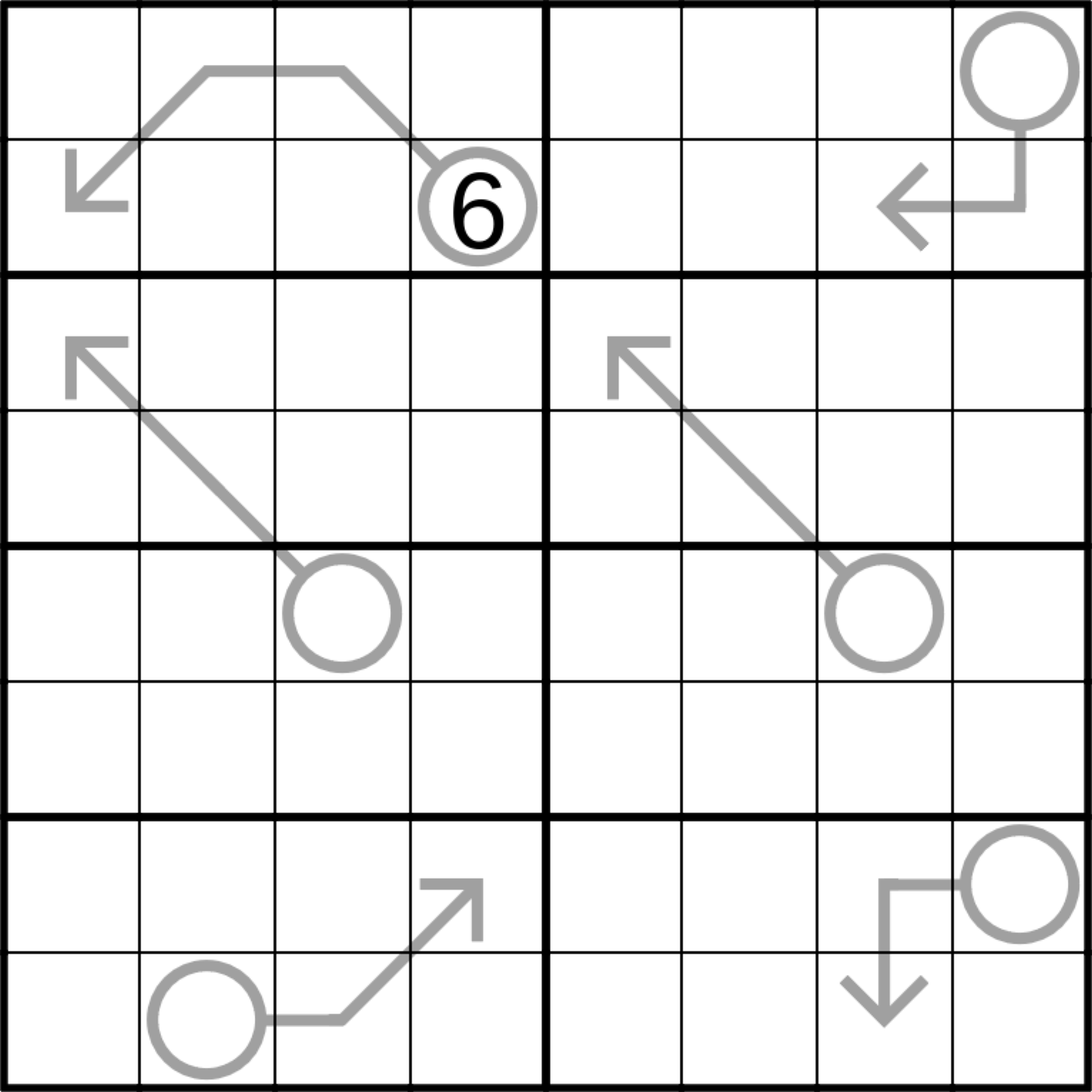
So here it is, my first Sudoku puzzle! Fletcher & Co.
You can play it online in SudokuPad.
Rules:
- Normal 8x8 sudoku rules apply.
- Digits along an arrow must sum to the digit in the arrow’s bulb.
- Any two orthogonally adjacent digits must be co-prime (i.e. their only common divisor must be 1).
What’s next?
Obviously I’d love to make a 10x10 with this constraint. I’ll need to spend some more time making sure that it can be done.
I hope you learnt something new! Happy solving!